$$ \ln(xy) = \ln(x) + \ln(y)$$
$$ \begin{align} a^4 + b^4 + c^4 + d^4 &= 16 \\ a^5 + b^5 + c^5 + d^5 &\overset{?}{\leq} 32 \end{align}$$
Düzlemde Bir Noktanın Bir Doğruya Olan Uzaklığı
Düzlemde Paralel Doğrular Arası Uzaklık
$$ \begin{align} \frac{d\left(x^x\right)}{dx} &= x^x \Bigl(\ln(x) + 1\Bigr) \end{align}$$
Devirli Sayılar Rasyonel Sayıya Nasıl Döner?
Wallis Çarpımı
$$ \begin{align} \frac{\pi}{2} &= \prod_{k = 1}^{\infty} \left(\frac{2k}{2k - 1} \cdot \frac{2k}{2k + 1}\right) \end{align}$$
Euler Çarpımı
$$ \begin{align} \text{sin}(x) &= x\prod_{k = 1}^{\infty} \left(1 - \frac{x^2}{k^2 \pi^2}\right) \end{align}$$
Euler Çarpımı ve π İle İlgili Sihirli Bağıntılar
$$ \begin{align} \frac{\pi}{4} &= \frac11 - \frac13 + \frac15 - \frac17 +... \end{align}$$
Özel İzafiyet Teorisi
$$ \begin{align} E &= m c^2 \end{align}$$
Merkezi Binom Katsayısı
(Asymptotic Form)
$$ \begin{align} \binom{2n}{n} \sim \frac{4^n}{\sqrt{n \pi}} \end{align}$$
$$ \begin{align} \frac{d\Bigl(\text{sin}(x)\Bigr)}{dx} &= \text{cos}(x) \end{align}$$
$$ \begin{align} \frac{d\Bigl(\text{cos}(x)\Bigr)}{dx} &= -\text{sin}(x) \end{align}$$
$$ \begin{align} \frac{d\Bigl(f(x) g(x)\Bigr)}{dx} &= f'(x)g(x) + f(x)g'(x) \end{align}$$
$$ \begin{align} \frac{d\Bigl(\frac{f(x)}{g(x)}\Bigr)}{dx} &= \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \end{align}$$
$$ \begin{align} \frac{d\Bigl(f\bigl(g(x)\bigr)\Bigr)}{dx} &= g'(x) f'\Bigl( g(x) \Bigr) \end{align}$$
$$ \begin{align} \frac{d\Bigl(\text{tan}(x)\Bigr)}{dx} &= \text{sec}^2(x) = 1 + \text{tan}^2(x) \end{align}$$
Trigonometrik Fonksiyonların Türevleri
Ters Trigonometrik Fonksiyonların Türevleri
$$ \begin{align} \frac{d\Bigl(a^x\Bigr)}{dx} &= a^x \ln(a) \end{align}$$
$$ \begin{align} \frac{d\Bigl(\log(x)\Bigr)}{dx} &= \frac{\log_{a}(e)}{x} \end{align}$$
$$ \begin{align} \frac{d\Bigl(W(x)\Bigr)}{dx} &= \frac{1}{e^{W(x)} + x} \end{align}$$
$$ \begin{align} \int W(x) dx &= x W(x) - x + e^{W(x)} \end{align}$$
$$ \begin{align} \eta(s) &= \Bigl( 1 - 2^{1 - s} \Bigr) \zeta(s) \end{align}$$
$$ \begin{align} \int_{0}^{1} x^m \ln^{n}(x) dx &= \frac{(-1)^n n!}{(m + 1)^{n + 1}} \end{align}$$
Laplace Gauss İntegralini Nasıl Çözdü?
$$ \begin{align} \int_{\mathbb{R}} e^{-x^2} dx &= \sqrt{\pi} \end{align}$$
Geometrik Serilerin Görsel İspatı
$$ \begin{align} \frac{1}{5} + \frac{1}{5^2} + \frac{1}{5^3} + ... &= \frac14 \end{align}$$
Geometrik Serilerin Görsel İspatı
$$ \begin{align} \frac{1}{4} + \frac{1}{4^2} + \frac{1}{4^3} + ... &= \frac13 \end{align}$$
Geometrik Serilerin Görsel İspatı
$$ \begin{align} \frac{1}{8} + \frac{1}{8^2} + \frac{1}{8^3} + ... &= \frac17 \end{align}$$
Geometrik Serilerin Görsel İspatı
$$ \begin{align} \frac{1}{3} + \frac{1}{3^2} + \frac{1}{3^3} + ... &= \frac12 \end{align}$$
Geometrik Serilerin Görsel İspatı
$$ \begin{align} \frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + ... &= 1 \end{align}$$
$$ \begin{align} 0,99999... &= 1 \end{align}$$
$$ \begin{align} 0! &= 1 \end{align}$$
$$ \begin{align} \ln(i) &= \frac{i \pi}{2} \end{align}$$
$$ \begin{align} i^i &= e^{-\pi / 2} \end{align}$$
Altın Oranın İrrasyonel Sayı Olduğunun Görsel İspatı
$$ \begin{align} \Phi &= \frac{1 + \sqrt{5}}{2} \end{align}$$
Aşağıdaki Bağıntının Görsel İspatı
$$ \begin{align} \sum_{k = 1}^{n} k^2 &= \frac{n(n + 1)(2n + 1)}{6}\end{align}$$
Euler Sayısının İrrasyonel Bir Sayı Olduğunun Matematiksel İspatı
$$ \begin{align} e &= \sum_{n = 0}^{\infty} \frac{1}{n!} \end{align}$$
Hangisi Euler Sayısına Daha Hızlı Yakınsar?
$$ \begin{align} e &= \sum_{n = 0}^{\infty} \frac{1}{n!} \\ e &= \lim_{n \rightarrow \infty}\left(1 + \frac{1}{n}\right)^n \end{align}$$
√2 Sayısının İrrasyonel Bir Sayı Olduğunun Görsel İspatı
$$ \begin{align} \sqrt{2} \longrightarrow \text{irrasyonel} \end{align}$$
Lambert W Fonksiyonunun Lagrange Açılımı
$$ \begin{align} W(y) &= \sum_{n=1}^{\infty} \frac{(-n)^{n-1} y^n}{n!} \end{align}$$
$$ \begin{align} \sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\text{.}^{\text{.}^{\text{.}}}}}} &= 2 \end{align}$$
$$ \begin{align} \sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\text{.}^{\text{.}^{\text{.}}}}}} &\neq 4 \end{align}$$
Pisagor Teoreminin Kalkülüs İspatı

$$ \begin{align} a^2 + b^2 &= c^2 \end{align}$$
Pisagor Teoreminin Görsel İspatı

$$ \begin{align} a^2 + b^2 &= c^2 \end{align}$$
$$ \begin{align} \sum_{k = 1}^{n} k &= \frac{n(n + 1)}{2} \end{align}$$
$$ \begin{align} \ln \Bigl( 2\text{sin}(x) \Bigr) &= -\sum_{n \geq 1} \frac{\text{cos}(2nx)}{n} \\ \ln \Bigl( 2\text{cos}(x) \Bigr) &= -\sum_{n \geq 1} \frac{(-1)^n\text{cos}(2nx)}{n} \end{align}$$
$$ \begin{align} \int_{0}^{\frac{\pi}{2}} \ln\Bigl(\text{cos}(x)\Bigr) dx &= -\frac{\pi}{2} \ln(2) \end{align}$$
$$ \begin{align} \int_{0}^{\frac{\pi}{2}} \ln\Bigl(\text{cos}(x)\Bigr) dx &= -\frac{\pi}{2} \ln(2) \end{align}$$
Alternatif ve Orjinal Çözüm
$$ \begin{align} \int_{0}^{\frac{\pi}{2}} \int_{0}^{\frac{\pi}{2}} \left( \frac{\text{sin}(x) + \text{sin}(y)}{\text{cos}(x) + \text{cos}(y)} \right)dx dy &= 4 \text{G} \end{align}$$
$$ \begin{align} \text{G} &\longrightarrow \text{Catalan's Constant} \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \hspace -5pt {\left( e^{- \alpha e^x} + e^{- \alpha e^{-x}} -1 \right) dx} &= - \ln\left( \alpha e^{\gamma} \right) \end{align}$$
$$ \begin{align} \gamma &\longrightarrow \text{Euler-Mascheroni Constant} \end{align}$$
Ramanujan Tekniği
$$ \begin{align} \Gamma(z) \Gamma(1 - z) &= \pi \text{csc}(\pi z) \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \left( \frac{\ln(x)}{e^x} \right) dx &= -\gamma \end{align}$$
$$ \begin{align} \gamma &\longrightarrow \text{Euler-Mascheroni Constant} \end{align}$$
$$ \begin{align} \sqrt{x + 1} &= \sum_{n = 2}^{\infty} \frac{x^n (-1)^{n - 1} (2n - 3)!}{2^{2n - 2} (n - 2)1 n!} \\ &+ \frac{x + 2}{2} \end{align}$$
$$ \begin{align} \text{Taylor Expansion} \end{align}$$
$$ \begin{align} \Gamma(z) &= \frac{e^{-\gamma z}}{z} \prod_{k = 1}^{\infty} \frac{k e^{z/k}}{k + z} \end{align}$$
Weierstrass Definition of Gamma Function
$$ \begin{align} \Gamma'(z) &= \Gamma(z) \Psi(z) \\ \Psi(z + 1) &= \Psi(z) + \frac{1}{z} \end{align}$$
$$ \begin{align} \Psi(z + 1) &= -\gamma + \sum_{n = 1}^{\infty} \left( \frac{1}{n} - \frac{1}{n + z} \right) \end{align}$$
$$ \begin{align} \Psi(z) &\longrightarrow \text{Digamma Function} \end{align}$$
$$ \begin{align} \sum_{n = 0}^{\infty} \left( \frac{1}{n^2 + 1} \right) &= \frac{\pi \: \text{coth}(\pi) + 1}{2} \end{align}$$
Birim hiperbol üzerindeki bir noktayı orjine bağlayan doğru ile hiperbol ve x ekseni arasında kalan bölgenin alanını veren bağıntının ispatı.

$$ \begin{align} S &= \frac{x}{2} \end{align}$$
$$ \begin{align} \sum_{k = 1}^{n} k \times k! &= (k + 1)! - 1 \end{align}$$
$$ \begin{align} B(z_1,z_2) &= \frac{\Gamma(z_1) \Gamma(z_2)}{\Gamma(z_1 + z_2)} \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \frac{x^{s - 1}}{1 + x^k} dx &= \frac{\pi}{k} \text{csc} \left( \frac{\pi s}{k} \right) \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \frac{x^{s - 1}}{1 - x^k} dx &= \frac{\pi}{k} \text{cot}\left(\frac{\pi s}{k}\right) \end{align}$$
$$ \begin{align} \Gamma(s)\zeta(s) &= \int_{0}^{\infty} \frac{x^{s - 1}}{e^x - 1} dx \end{align}$$
$$ \begin{align} 4 \mid \left(3^n + 7^n - 2\right) \: , \: \forall n \in \mathbb{N} \end{align}$$
Geometrik İspat
$$ \begin{align} \frac{2ab}{a + b} &\leq \sqrt{ab} \leq \frac{a + b}{2} \leq \sqrt{\frac{a^2 + b^2}{2}} \end{align}$$
Geometrik İspat
$$ \begin{align} \text{cos}(x + y) &= \text{cos}(x)\text{cos}(y) - \text{sin}(x)\text{sin}(y) \\
\text{sin}(x + y) &= \text{sin}(x)\text{cos}(y) + \text{sin}(y)\text{cos}(x)
\end{align}$$
Dirichlet Kernel Formula
$$ \begin{align}
\sum_{k = -n}^{n} e^{ikx} &= \frac{\text{sin}\left(\left( n + \frac12 \right)x\right)}{\text{sin}\left( \frac{x}{2} \right)} \\
\sum_{k = -n}^{n} e^{ikx} &= 1 + 2 \sum_{k = 1}^{n} \text{cos}(kx)
\end{align}$$
$$ \begin{align}
\eta(0) &= \frac12
\end{align}$$
$$ \begin{align}
\eta'(0) = \frac12 \ln \left( \frac{\pi}{2} \right)
\end{align}$$
$$ \begin{align}
\int_{-\infty}^{\infty} e^{-x^2} dx &= \sqrt{\pi}
\end{align}$$
$$ \begin{align}
s &\in \mathbb{R}^{+}
\end{align}$$
$$ \begin{align}
\int_{0}^{\infty} \frac{dx}{\left( e^{x} + e^{-x} \right)^s} &= \frac{\Gamma^2\left(\frac{s}{2}\right)}{4\Gamma(s)}
\end{align}$$
$$ \begin{align}
\Psi(1/2) &= -\gamma - 2 \ln(2) \\
\Gamma'(1/2) &= -\sqrt{\pi} \bigl( \gamma + 2 \ln(2) \bigr)
\end{align}$$
$$ \oint\limits_{|z| = R} z^n dz =
\begin{cases}
0 & , & n \neq -1 \\
2 \pi i R^{n + 1} & , & n = -1
\end{cases}$$
$$ \begin{align}
\mathbb{P} &= \{2,3,5,7,11,... \}
\end{align}$$
Asal Sayılar
Sonlu Mu? Sonsuz Mu?
$$ \begin{align}
1 + 2 + 3 + 4 + 5 + 6 \; + \; ... &= -\frac{1}{12}
\end{align}$$
$$ \left. \begin{align}
x,y,z &> 0 \\
x + y + z &= 1
\end{align} \right \} \Rightarrow \frac{1}{x} + \frac{1}{y} + \frac{1}{z} > 3$$
$$ \begin{align}
n \in \mathbb{Z} &\Rightarrow \frac{n}{6} + \frac{n^2}{2} + \frac{n^3}{3} \in \mathbb{Z}
\end{align}$$
$$ \begin{align}
\operatorname{Li}_{2}\Bigl(-z\Bigr) + \operatorname{Li}_{2}\Bigl(-\frac{1}{z}\Bigr) &= f(z)
\end{align}$$
$$ \begin{align}
\operatorname{Li}_{3}\Bigl(-z\Bigr) - \operatorname{Li}_{3}\Bigl(-\frac{1}{z}\Bigr) &= g(z)
\end{align}$$
$$ \begin{align}
f(z) &= -\frac{\ln^2(z)}{2} - \frac{\pi^2}{6}
\end{align}$$
$$ \begin{align}
g(z) &= -\frac{\ln^3(z)}{6} - \frac{\pi^2 \ln(z)}{6}
\end{align}$$
$$ \begin{align}
\frac{1}{1999} < \frac12 \cdot \frac34 \cdot \frac56 ... \frac{1997}{1998} &< \frac{1}{44}
\end{align}$$
$$ 2\sqrt[3]{2x + 1} = x^3 - 1$$
$$ 4^{\frac{1}{x}} + 6^{\frac{1}{x}} = 9^{\frac{1}{x}}$$
$$ x^x = \frac{1}{\sqrt{2}}$$
$$ x^{2x^2 - 22x + 60} = 1$$
$$ \left(1 + \frac{1}{x}\right)^{x + 1} = \left(1 + \frac{1}{2021}\right)^{2021}$$
$$ \begin{align} &2^a = 3^b = 7^c = 42 \\ &\Rightarrow \frac{1}{a} + \frac{1}{b} + \frac{1}{c} = ? \end{align}$$
$$ \frac{(x + 1)^5}{x^5 + 1} = \frac{81}{11}$$
$$ \text{log}_{3}(a + 1) = \text{log}_{4}(a + 8)$$
$$ \sqrt{x - \sqrt{x - ...}} = \sqrt{1 + \sqrt{1 + ...}}$$
$$ x^2 + \frac{81x^2}{(x + 9)^2} = 40$$
$$ x^4 + x^3 + x^2 + x + 1 = 0$$
$$ \sqrt[7]{x} - \sqrt[5]{x} = \sqrt[3]{x} - \sqrt{x}$$
$$ \begin{align} &\sqrt{x} + y = 7 \\ &x + \sqrt{y} = 11 \end{align}$$
$$ \begin{align} &xyz = 103(x + y + z) \end{align}$$
$$ \begin{align} &x^2 - 2y^2 = 1 \end{align}$$
$$ \begin{align} &\frac{1}{x} - \frac{1}{y} = \frac{1}{x + y} \\ &\Rightarrow \frac{y}{x} = ? \end{align}$$
$$ \begin{align} &2^x = 3^{\frac{x}{2}} + 1 \end{align}$$
$$ \begin{align} &a^4 + b^4 + c^4 + d^4 = 4abcd \end{align}$$
$$ \begin{align} &\left(x^2 + x + 1\right)^2 = x^2\left(3x^2 + x + 1\right) \end{align}$$
$$ \begin{align} &\left(\sqrt{x} \right)^{x} = x^{\sqrt{x}} \end{align}$$
$$ \begin{align} &x^{-x^{1 - x}} = 2^8 \end{align}$$
$$ \begin{align} &xy' + 2y = x^3 \end{align}$$
$$ \begin{align} &n^2 + 19n - n! = 0 \end{align}$$
$$ \begin{align} &\ln\left(x^2 + x\right) = \ln\left(x^2\right) + \ln(x) \end{align}$$
$$ \begin{align} &x^{\text{log}(x)} = 10^{2025} \end{align}$$
$$ \begin{align} &y = \left(\frac{dy}{dx}\right)^2 \end{align}$$
$$ \begin{align} &y' = (x + y)^2 \end{align}$$
$$ \begin{align} &117y^3 - x^3 = 5 \end{align}$$
$$ \begin{align} &\left\{ x,\frac{x}{x - 2},\frac{x}{x - 4},\frac{x}{x - 6} \right\} \in \mathbb{Z} \end{align}$$
$$ \begin{align} &5^x - 3^x = 16 \end{align}$$
$$ \begin{align} x^2 + y^2 &= x + y - \frac12 \end{align}$$
$$ \begin{align} \text{tan}(x) &= 3\text{cos}(x) \\ \text{sin}(x) &= ? \end{align}$$
$$ \begin{align} e^x = e x \end{align}$$
$$ \begin{align} \Bigl ( \text{sin}(y) \Bigr)^{2022} - x^{2022} = 1 \end{align}$$
$$ \begin{align} 2^x + x &= 11 \end{align}$$
$$ \begin{align} 6^x + 6^y &= 42 \\ x + y &= 3 \end{align}$$
$$ \begin{align} \Bigl ( \text{sin}(x) \Bigr)^{\text{sin}(x)} &= 2\end{align}$$
$$ \begin{align} \left( \sqrt{100 + \sqrt{n}} + \sqrt{100 - \sqrt{n}} \right) &\in \mathbb{Z} \end{align}$$
$$ \begin{align} \Rightarrow \text{min}\{n\} \in \mathbb{Z}^{+} &= ? \end{align}$$
$$ \begin{align} \sqrt[3]{x} + \sqrt[3]{x - 16} &= \sqrt[3]{x - 8} \end{align}$$
$$ \begin{align} \left(x - \frac{1}{x}\right)^{\frac12} + \left(1 - \frac{1}{x}\right)^{\frac12} &= x \end{align}$$
$$ \begin{align} x^4 + 2x^2 + x + 2 &= 0 \end{align}$$
$$ \begin{align} x^{2021} &= x^{2020} + 1 \end{align}$$
Bu denklemin en az iki karmaşık kökünün olduğunu gösterebilir misiniz?
$$ \begin{align} \text{sin}^2(x) + \text{cos}^3(x) &= \frac78 \end{align}$$
$$ \begin{align} n! &= n^3 - n \end{align}$$
$$ \begin{align} x! + y! + z! &= w! \end{align}$$
$$ \begin{align} 2^{\text{sin}^2(x)} + 2^{\text{cos}^2(x)} &= 3 \end{align}$$
$$ \begin{align} \frac{1 + r + r^2 + r^3 +...}{1 + r^3 + r^6 + r^9 +...} &= \frac74 \end{align}$$
$$ \begin{align} \frac{dy}{dx} &= \frac{x - y}{x + y} \end{align}$$
$$ \begin{align} p,q &\in \mathbb{Z}^{+} \\ \frac{1}{p} + \frac{1}{q} + \frac{1}{pq} &= \frac14 \end{align}$$
$$ \begin{align} x^3 + 3x^2 - 24x + 1 &= 0 \end{align}$$
$$ \begin{align} \text{Ç} &= \{\alpha,\beta,\gamma \} \end{align}$$
$$ \begin{align} \sqrt[3]{\alpha} + \sqrt[3]{\beta} + \sqrt[3]{\gamma} &= ? \end{align}$$
$$ \begin{align} \text{sin}(\theta) &= 2 \end{align}$$
$$ \begin{align} \Bigl(\ln(x)\Bigr)^{\ln(x)} &= \ln\Bigl(x^{\ln(x)}\Bigr)\end{align}$$
$$ \begin{align} \sqrt{2 - \sqrt{x + 2}} &= x \end{align}$$
$$ \begin{align} \frac{dx}{dt} &= xy \\ \frac{dy}{dt} &= y + 1 \\ &\Rightarrow x,y = ? \end{align}$$
$$ \begin{align} \text{sin}\Bigl(\text{cos}(x)\Bigr) &= \text{cos}\Bigl(\text{sin}(x)\Bigr) \end{align}$$
$$ \begin{align} \sqrt{x} + \sqrt{-x} &= 2 \end{align}$$
$$ \begin{align} \ln\Bigl(\ln(x)\Bigr) &= \log\Bigl(\log(x)\Bigr) \end{align}$$
$$ \begin{align} \log\Bigl(\ln(x)\Bigr) &= \ln\Bigl(\log(x)\Bigr) \end{align}$$
$$ \begin{align} 16^{x^2 + y} + 16^{x + y^2} &= 1 \end{align}$$
$$ \begin{align} \frac{1}{1 + \text{cos}^2(x)} + \frac{1}{1 + \text{sin}^2(x)} &= \frac{48}{35} \end{align}$$
$$ \begin{align} x,y \in \mathbb{Z} \end{align}$$
$$ \begin{align} \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{y}} &= \frac{1}{\sqrt{20}} \end{align}$$
$$ \begin{align} \frac{1}{2!9!} + \frac{1}{3!8!} + \frac{1}{4!7!} + \frac{1}{5!6!} &= \frac{n}{10!} \end{align}$$
$$ \begin{align} \log_{7}(x) + \log_{8}(x) &= 1 \end{align}$$
$$ \begin{align} x^5 - x^4 - x^2 &= 5x^3 + 6x \end{align}$$
$$ \begin{align} \frac{y''}{\left(y'\right)^2} &= \frac{y}{y^2 - 1} \\ y &= ? \end{align}$$
$$ \begin{align} i^x &= -1 \\ x &= ? \end{align}$$
$$ \begin{align} e^x &= x^e \\ x &= ? \end{align}$$
$$ \begin{align} (1 + i)^x &= 16 \\ x &= ? \end{align}$$
$$ \begin{align} \frac{1}{x^3} - \frac{1}{(x + 1)^3} &= \frac78 \\ x &= ? \end{align}$$
$$ \begin{align} x^{x^{\ln(x)}} &= e^e \\ x &= ? \end{align}$$
$$ \begin{align} x^x &= 2^{3x + 192} \\ x &= ? \end{align}$$
$$ \begin{align} e^{e^x} &= 1 \\ x &= ? \end{align}$$
$$ \begin{align} i^x &= 2 \\ x &= ? \end{align}$$
$$ \begin{align} 2^x + x &= 5 \\ x &= ? \end{align}$$
$$ \begin{align} 2^{x^{x^{x^{\text{.}^{\text{.}^{\text{.}}}}}}} \\ x &= ? \end{align}$$
$$ \begin{align} \sqrt{16 - x^2} + \sqrt{9 - x^2} &= 5 \\ x &= ? \end{align}$$
$$ \begin{align} y' + \frac{1}{y} y'' &= 0 \\ y &= ? \end{align}$$
$$ \begin{align} p,q,r &\rightarrow \text{Constant Coefficients} \end{align}$$
$$ \enclose{bottom} {\begin{array}{1c1c1c1c1c1c}
p \color{crimson}y'' & + & q \color{navy}y' & + & r \color{green}y & = & 0 \\
p \color{crimson}m^2 & + & q \color{navy}m^1 & + & r \color{green}m^0 & = & 0
\end{array}}$$
$$ \begin{align}
y &= C_1 e^{m_1 x} + C_2 e^{m_2 x} \\
m_{1,2} &= \frac{-q \pm \sqrt{q^2 - 4pr}}{2p}
\end{align}$$
$$ \begin{align} 2x^4 - 13x^3 + 24x^2 - 13x + 2 &= 0 \end{align}$$
$$ \begin{align} (x + 7)^7 &= x^7 + 7^7 \end{align}$$
Diyafont Denklemler
$$ \begin{align} \sqrt{x - \sqrt{y}} + \sqrt{x + \sqrt{y}} &= \sqrt{xy} \end{align}$$
$$ \begin{align} \Biggl( \frac{1 + a^2}{2a} \Biggr)^{x} - \Biggl( \frac{1 - a^2}{2a} \Biggr)^{x} &= 1 \end{align}$$
$$ \begin{align} 0 < a < 1 \: &\wedge \: x \in \mathbb{R} \end{align}$$
$$ \sqrt[3]{8 + 3\sqrt{21}} + \sqrt[3]{8 - 3\sqrt{21}} = ?$$
$$ \sqrt{70 \times 71 \times 72 \times 73 + 1} = ?$$
$$ \begin{align} &a + b + c = 0 \\ &\Rightarrow \frac{a^7 + b^7 + c^7}{abc\left(a^4 + b^4 + c^4\right)} = ? \end{align}$$
$$ \begin{align} &\sqrt{\frac{1111111088888889}{123456787654322 - 1}} = ? \end{align}$$
$$ \begin{align} &\sqrt{\frac{2021^3 - 2019^3 - 2}{6}} = ? \end{align}$$
$$ \begin{align} &\left(\frac{1 + \sqrt{5}}{2}\right)^8 + \left(\frac{1 - \sqrt{5}}{2}\right)^8 = ? \end{align}$$
$$ \begin{align} a + b &= 3 \\ a^2 + b^2 &= 7 \\ a^6 + b^6 &= ? \end{align}$$
$$ \begin{align} \frac{x}{x^2 + x + 1} &= a \\ \frac{x^2}{x^4 + x^2 + 1} &= ? \end{align}$$
$$ \begin{align} \int \sqrt{x^2 - 2x} dx &= ? \end{align}$$
$$ \begin{align} \text{min}\left \{ \frac{1}{\text{sin}^2(x)} + \frac{1}{\text{cos}^2(x)} \right \} &= ? \end{align}$$
$$ \begin{align} m^2 &= n + 2 \\ n^2 &= m + 2 \\ m &\neq n \end{align}$$
$$ \begin{align} &\Rightarrow 4mn - m^3 - n^3 = ? \end{align}$$
$$ \begin{align} P(x) &= ax^7 + bx^3 + 2 \\ P(11) &= 5 \\ P(-11) &= ? \end{align}$$
Aşağıdaki bağıntıları sağlayan geometrik dizinin ilk üç elamanı nedir?
$$ \begin{align} a_1 + a_2 + a_3 &= 21 \\ a_{1}^{2} + a_{2}^{2} + a_{3}^{2} &= 189 \end{align}$$
$$ \begin{align} \int \frac{\left(1 - x^n\right)}{x\left(1 + x^n\right)} dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} \frac{x^4 (1 - x)^4}{1 + x^2} dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \ln\left(\frac{e^x + 1}{e^x - 1}\right) dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \frac{\text{sin}(x)}{x} dx &= ? \end{align}$$
$$ \begin{align} \int_{-\infty}^{\infty} \frac{\text{sin}^2(x)}{x^2} dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} (-1)^x dx &= ? \end{align}$$
$$ \begin{align} a_{2n} &= a_2 a_n + 1 \\ a_{2n + 1} &= a_2 a_n - 2 \\ a_7 &= 2 \\ 0 &< a_1 < 1 \\ a_{25} &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} \frac{x^7 - 1}{\ln(x)} dx &= ? \end{align}$$
$$ \begin{align} \Bigl(a\Bigr)^{\frac{\ln\bigl(\ln(a)\bigr)}{\ln(a)}} &= ? \end{align}$$
$$ \begin{align} \int_{a}^{b} \frac{f(x)}{f(a + b - x) + f(x)} dx &= ? \end{align}$$
$$ \begin{align} f(x) &= \int_{1}^{x} \frac{dt}{\sqrt{t^3 + 2t^2 + 1}} \\ &\Rightarrow \left(f^{-1}\right)'(0) = ? \end{align}$$
$$ \begin{align} \sum_{n = 1}^{\infty} \frac{1}{\Bigl(a + (n - 1)r\Bigr)\Bigl(a + nr\Bigr)} &= ? \end{align}$$
$$ \begin{align} x \in (-1,1) \end{align}$$
$$ \begin{align} \sqrt{1 + 2x + 3x^2 + 4x^3 + ...} &= ? \end{align}$$
$$ \begin{align} e^{e^{e^{\text{.}^{\text{.}^{\text{.}}}}}} &= ? \end{align}$$
$$ \begin{align} 3\sqrt{2} - \sqrt{7 - 3\sqrt{5}} &= ? \end{align}$$
$$ \begin{align} 2 \overset{?}{=} 1 \end{align}$$
$$ \begin{align} \sqrt{-4}\sqrt{-25} &= ? \end{align}$$
$$ \begin{align} (1,999)^4 \approx ? \end{align}$$
$$ \begin{align}
a &= \sum_{n = 0}^{\infty} \left( \sqrt{n} - \sqrt{n + 1} \right) \\
b &= \sum_{n = 0}^{\infty} \frac{(-1)^n}{n + 1} \\
c &= \lim_{t \rightarrow \infty} \left(1 + \frac{1}{e^t}\right)^{e^t} \\
d &= \frac{d}{dx}\left(\frac{x^2}{\text{sin}^2(x) + \text{cos}^2(x)}\right)
\end{align}$$
$$ \begin{align} \left(\int_{a}^{b} c^d dx\right)^2 &= ? \end{align}$$
$$ \begin{align} \sqrt{x + yi} &= ? \end{align}$$
$$ \begin{align} \sum_{n = 2}^{\infty} \log\left(\frac{n^3 - 1}{n^3 + 1}\right) &= ? \end{align}$$
$$ \begin{align} \sqrt{(1000)(1001)(1002)(1003) + 1} &= ? \end{align}$$
$$ \begin{align} x + y = x^2 + y^2 = x^3 + y^3 &= ? \end{align}$$
$$ \begin{align} n < 4 \: \wedge \: n \in \mathbb{Z}^{+} \end{align}$$
$$ \begin{align} x^n + y^n + z^n &= n \\ x^4 + y^4 + z^4 &= ? \end{align}$$
$$ \begin{align} \lim_{x \rightarrow 0} \left(\frac{1 - \text{cos}(x)}{x}\right) &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} \left(x^{x}\right)^{\left(x^{x}\right)^{\left(x^{x}\right)^{\left(...\right)}}} dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} x^{-x} dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\frac{\pi}{2}} \text{tan}^{i}(x) dx &= ? \end{align}$$
$$ \begin{align} \int_{\mathbb{R}} \left(\frac{\text{cos}(x)}{\text{cosh}(x)}\right) dx &= ? \end{align}$$
$$ \begin{align} P(x) = 2x^5 &- 22x^4 - 47x^3 + \\ &- 67x^2 + 29x + 2 \end{align}$$
Yukarıdaki polinomun (𝑥 - 13) ile bölümünden kalan nedir?
$$ \begin{align} \int_{0}^{\infty} e^{-x^2} \text{cos}(5x) dx &= ? \end{align}$$
$$ \begin{align} \sqrt{2 \sqrt[3]{2 \sqrt[4]{2 \sqrt[5]{2 \: \text{...}}}}} &= ? \end{align}$$
$$ \begin{align} \int_{-2}^{1} \left(\frac{1}{x^2}\right) dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} x^x dx &= ? \end{align}$$
$$ \begin{align} \sqrt[3]{3}^{\sqrt[3]{3}^{\sqrt[3]{3}^{\text{.}^{\text{.}^{\text{.}}}}}} &= ? \end{align}$$
$$ \begin{align} \sqrt[3]{7 + \sqrt{50}} + \sqrt[3]{7 - \sqrt{50}} &= ? \end{align}$$
$$ \begin{align} \sum_{n = 1}^{\infty} \text{arctan}\left(\frac{\sqrt{3}}{3n^2 + 3n + 1}\right) &= ? \end{align}$$
$$ \begin{align} a &= \int_{0}^{\infty} \sqrt{t} e^{-t} dt \\ S_n &= \sum_{n = 0}^{\infty} \frac{x^{4n + 4}}{(2n + 1)(4n + 3)(4n + 4)} \end{align}$$
$$ \begin{align} \lim_{x \rightarrow a} \left( S_n \right)'' &= ? \end{align}$$
$$ \begin{align} \int \left( \frac{1}{1 + \text{sin}(x) + \text{cos}(x)} \right) dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \text{cos}\left(x^2\right) dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \text{sin}\left(x^2\right) dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} \frac{dx}{\sqrt{1 - x^2}} \ln\left(\frac{\sqrt{1 + x} + 1}{\sqrt{1 + x} - 1}\right) &= ? \end{align}$$
$$ \begin{align} \int \frac{dx}{\sqrt{x}\sqrt{x^2 + 1}\sqrt{x + \sqrt{x^2 + 1}}} &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \left( \frac{\ln(x)}{1 + e^x} \right) dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \left( \frac{e^{-x} \bigl( 1 - \text{cos}(x) \bigr)}{x^2} \right) dx &= ? \end{align}$$
Feynman Tekniği
$$ \begin{align} \int_{0}^{\infty} \left( \frac{e^{-x} \bigl( 1 - \text{cos}(x) \bigr)}{x^2} \right) dx &= ? \end{align}$$
Taylor Serileri ve Laplace Dönüşümleri
$$ \begin{align} \int_{0}^{1} \ln^{3} \left( \frac{1 - x}{1 + x} \right) dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} \text{cos}\Bigl(\ln(x) \Bigr) \frac{x^{\alpha} - x^{\beta}}{\ln(x)} dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \frac{\text{cos}\Bigl(\ln(x) \Bigr)}{1 + x + x^2} dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \frac{\text{sin}\Bigl(2\ln^2(x) \Bigr)}{(1 + x) \ln^2(x)} dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} \text{sin}\left(\sqrt{-ln(x)} \right) dx &= ? \end{align}$$
$$ \begin{align} \int_{-\infty}^{\infty} \Gamma(1 + ix) \Gamma(1 - ix) dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} \frac{\left(x^{\Phi} - 1\right)^2}{\ln^2(x)} dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \frac{\ln(x)}{1 + x^2} dx &= ? \end{align}$$
$$ \begin{align} \frac{\zeta(2)}{\alpha^2} + \frac{\zeta(3)}{\alpha^3} + \frac{\zeta(4)}{\alpha^4} + ... &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} \sqrt{\frac{x}{1 - x}} \ln\left( \frac{x}{1 - x} \right) dx &= ? \end{align}$$
$$ \begin{align} P\bigl(P(x) - 1\bigr) &= x^{16} + 1 \end{align}$$
$$ \begin{align} P(2) &= ? \end{align}$$
$$ \begin{align} A &= 1000! \end{align}$$
A sayısı kaç basamaklı bir sayıdır?
$$ \begin{align} \int_{0}^{1} \frac{\left(x^{s} - 1\right) dx}{\left(1 + x + x^2 + ... + x^{k - 1} \right) \ln(x)} &= ? \end{align}$$
$$ \begin{align}
\int_{0}^{1} \ln \left( \ln \left( \frac{1}{x} \right) \right) \frac{1}{(1 + x)^2} dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\infty} \left( \frac{e^{-ax} \text{sin}(bx)}{x} \right) dx &= ?
\end{align}$$
$$ \begin{align}
a \in \mathbb{R} &> 0
\end{align}$$
$$ \begin{align}
\int_{0}^{1} \Psi(x) \text{sin}(\pi x) \text{cos}(\pi x) dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\infty} \Gamma^{2}\bigl(1 - ix^2 \bigr) \Gamma^{2}\bigl(1 + ix^2 \bigr) dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\pi/2} \left( \frac{\text{arctan}\left( 2 \text{cos}^2(x) \right)}{\text{cos}^2(x)} \right) dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{1} \bigl (\text{arcsin}(x) \bigr)^2 \ln(x) dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\infty} \left( \frac{x^2}{\text{cosh}^2 (x^2)} \right) dx &= ?
\end{align}$$
$$ \begin{align}
\LARGE \int \normalsize \left(\sqrt{\frac{\text{tan}(x)}{\sqrt{\frac{\text{tan}(x)}{\sqrt{\frac{\text{tan}(x)}{\text{...}}}}}}} \right) dx &= ?
\end{align}$$
$$ \begin{array}{1c1c1c1c}
-1 &\leq &\text{sin}(\theta) &\leq &+1 \\
-1 &\leq &\text{cos}(\theta) &\leq &+1 \\
? &\leq &\text{sin}(\theta) + \text{cos}(\theta) &\leq &?
\end{array}$$
$$ \begin{align}
\int_{0}^{\infty} \frac{dx}{1 + x^{80}} &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\infty} e^{-ax^2} \text{sin}(bx^2) dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\pi/2} \frac{x}{\text{tan}(x)} dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\infty} \frac{\text{arctan}(x)}{x(x + 1)(x^2 + 1)} dx &= ?
\end{align}$$
$$ \begin{align}
\int_{\alpha}^{\alpha + 1} \ln\bigl( \Gamma(z) \bigr) dz &= ?
\end{align}$$
$$ \begin{align}
\alpha &\geq 0
\end{align}$$
$$ \begin{align}
\int_{0}^{1} \frac{\ln(x) \ln\bigl( -\ln(x) \bigr)}{1 - x} dx &= ?
\end{align}$$
$$ \begin{align}
\sum_{n = 0}^{\infty} \frac{n!}{(2n + 1)!} &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\pi/2} \frac{\text{arctan}\bigl(2 \text{cos}^2(x)\bigr)}{\text{cos}^2(x)} dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\pi/2} \frac{\text{sin}(x) \ln\bigl(\text{sin}(x)\bigr)}{\sqrt{1 + \text{sin}^2(x)}} dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{2\pi} e^{\text{cos}(\theta)} d \theta &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\pi/4} \frac{\ln\bigl( 1 - \text{tan}(x) \bigr)}{\text{tan}(x)} dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\infty} \text{arctan}^2\left(\frac{1}{x}\right) dx &= ?
\end{align}$$
$$ \begin{align}
\int_{-\pi/2}^{+\pi/2} e^{-\text{tan}^2(x)} dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{1} \frac{x(1 + x)}{x^2 - x + 1} \ln\bigl( -\ln(x) \bigr) dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{1} \frac{1 + x^2}{x^2} \ln(x) \ln(1 + x^2) dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\infty} \normalsize \ln\left( \frac{1}{x^{n} \ln \left( \frac{1}{x^{n} \ln \left( \frac{1}{x^{n} \ln (...)} \right)} \right)}\right) dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\pi/4} \frac{\text{cos}(2x)}{\ln(\text{tan}(x)) \text{cos}^4(x)} dx &= ?
\end{align}$$
$$ \begin{align}
\int_{1}^{\infty} \frac{\text{sin}^2 \bigl( \ln(x) \bigr)}{x^2 \ln^{2}(x)} dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\infty} \frac{x^{s}}{e^{x - t} - 1} dx &= ?
\end{align}$$
$$ \begin{align}
t &< 0
\end{align}$$
$$ \begin{align}
\int_{0}^{\pi} e^{2\text{cos}(x)} d x &= ?
\end{align}$$
$$ \begin{align}
\int_{-\infty}^{+\infty} \text{arctan}(e^{x}) \text{arctan}(e^{-x}) d x &= ?
\end{align}$$
$$ \begin{align}
\sum_{n = 0}^{\infty} \frac{n}{(n + 1)! + n!} &= ?
\end{align}$$
Alternatif Çözüm
$$ \begin{align}
\sum_{n = 0}^{\infty} \frac{n}{(n + 1)! + n!} &= ?
\end{align}$$
Part I
$$ \begin{align}
\int_{0}^{\pi/2} e^{-\text{tan}(\theta)} d \theta &= ?
\end{align}$$
Part II
$$ \begin{align}
\int_{0}^{\pi/2} e^{-\text{tan}(\theta)} d \theta &= ?
\end{align}$$
Part III
$$ \begin{align}
\int_{0}^{\pi/2} e^{-\text{tan}(\theta)} d \theta &= ?
\end{align}$$
$$ \begin{align}
\sum_{n = 1}^{\infty} \zeta(2n) x^{2n} &= ?
\end{align}$$
$$ \begin{align}
\sum_{k = 1}^{\infty} \frac{(-1)^k \text{sin}(k)}{k^3} &= ?
\end{align}$$
Dairenin yarıçapı nedir?

Boyalı bölgenin alanı nedir?

Koninin yüksekliği nedir?

𝑥 uzunluğu nedir?

A ile R arasındaki bağıntı nedir?

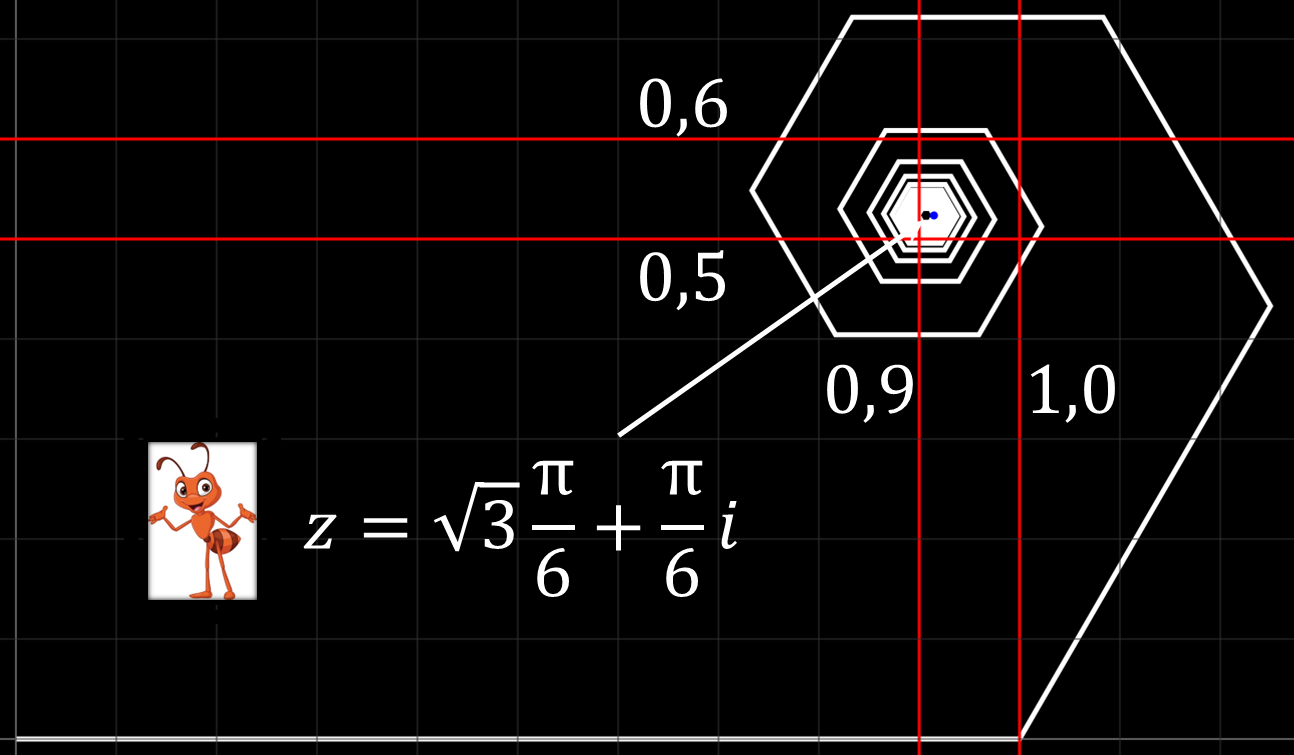
Yüksekliğin(y) en büyük değeri nedir?

$$ \alpha + \beta = ?$$

Dairenin yarıçapı nedir?

Gölgenin dikey uzunluğu(𝑥) nedir?

Boyalı bölgenin alanı nedir?

Küçük tekerlek kaç tur döner?

Alanların toplamı nedir?

Boyalı bölgenin alanı nedir?

|BD| uzunluğu nedir?

𝑥 uzunluğu nedir?

Açının değeri nedir?

Açının değeri nedir?

Boyalı bölgenin alanı nedir?

Boyalı bölgenin alanı nedir?

|DC| uzunluğu nedir?

Minimum değeri nedir?

Açının değeri nedir?

Açıların toplamı nedir?

Boyalı bölgenin alanı nedir?

Sarıya boyalı bölgenin alanı nedir?

Maviye boyalı bölgenin alanı nedir?

Yarım dairenin alanı nedir?

ABCD bir dikdörtgendir. |AD| uzunluğu 8 ve |KM| uzunluğu 6 ise |DC| uzunluğu nedir?

Maviye boyalı bölgenin alanı nedir?

Boyalı dik üçgenin alanı nedir?

Boyalı tam dairenin alanı nedir?

Boyalı karenin alanı nedir?

|CD| uzunluğu nedir?

En küçük dairenin yarıçapı nedir?

Dik üçgenin alanı nedir?

$$ \begin{align} |AB| &= \sqrt{x} + \sqrt{y} \\ x &< y \end{align}$$
𝑥 ve y doğal sayılarını bulun?

Karenin alanı nedir?

En büyük dairenin yarıçapı nedir?

|AB| uzunluğu ve karenin alanı nedir?

Üçgenin alanı nedir?

Her durum için direkler arası mesafe nedir?

Boyalı bölgenin alanı nedir?

Mavi açının değeri nedir?

Özdeş dairelerin yarıçapı nedir?

Boyalı dik üçgenin alanı nedir?

Boyalı karenin alanı nedir?

En büyük dairenin merkez noktası nedir?

Soru işaretli açı kaç derecedir?

Dairenin yarıçapı nedir?

Dış teğet çemberin yarıçapı nedir?

Herhangi bir üçgenin içerisinde bir nokta belirliyoruz ve bu noktayı köşelerle birleştiriyoruz. Bu noktanın köşelere olan uzaklıklarına eşit kenar uzunluklarına sahip bir üçgen çiziyoruz. Çizdiğimiz bu üçgenin iç açılarının parametrik gösterimi nedir?

Soru işaretli uzunluk nedir?

Soru işaretli uzunluk nedir?

𝑥 açısının değeri kaçtır?

Hangisinin çevresi daha büyüktür?

Yıldızın iç açıları toplamı nedir?

Bu işte bir terslik var!

Sarıya boyalı açının değeri nedir?

Sarıya boyalı açının değeri nedir?

Boyalı bölgenin alanı nedir?

Daire merkezleri arasındaki mesafe nedir?

Soru işaretli bölgenin alanının parametrik gösterimi nedir?

ABCD bir paralelkenardır. Çokgenin alanının paralelkenarın alanına oranı nedir?

$$ \begin{align} |ED| &= 7 \\ |EC| &= 24 \\ |FA| &= 15 \\ |AD| &= ? \end{align}$$
AD uzunluğu nedir?

𝑥 değeri kaçtır?

$$ \begin{align} |BD| &= 6 \\ |AC| &= 8 \\ |KL| &= ? \end{align}$$
KL uzunluğu nedir?

Teğet noktalarının parametrik gösterimi nedir?

$$ \begin{align} |BC| &= 10 \end{align}$$
ABDC dörtgeninin alanı nedir?

Sarı açının değeri nedir?

𝑥 uzunluğunun değeri nedir?

Sarı açının değeri nedir?

Düzgün altıgenin alanı nedir?

$$ \begin{align} A(\overset{\unicode{x25A0}}{ABCD}) &= 50 \end{align}$$
ABCD bir kare ise sarıya boyalı karenin alanı nedir?

ABCD ve EFGH birer karedir. Bu durumda CG uzunluğu nedir?

$$ \begin{align} |EC| &= 2 |EB| \end{align}$$
𝑥 açısının değeri nedir?

𝑥 açısının değeri nedir?

𝑥 açısının değeri nedir? (Bir önceki sorunun alternatif çözümü.)

Boyalı bölgenin alanı nedir?

$$ \begin{align} S_1 - S_2 &= 36 \\ |KL| &= ? \end{align}$$
KL uzunluğu nedir?

Boyalı bölgenin alanı 20 ise AB uzunluğu nedir?

$$ \begin{align} |AC| + |BL| &= 12 \\ |AC| &= |BC| \\ m(\widehat{LBK}) &= 2 \times m(\widehat{CKL}) \end{align}$$
ABC üçgeninin çevresi nedir?

KL(𝑥) uzunluğunun değeri nedir?

Birim karelerde oluşan şekilde boyalı bölgenin alanı nedir?

Sarıya boyalı açının değeri nedir?

Alanı 6 olan özdeş 4 adet eşkenar üçgen yanyana şekildeki gibi yerleştirilmiştir. Boyalı bölgenin alanı nedir?

$$ \begin{align} |AM| &= |AB| \\ |AT_1| &= 10 \\ |DT_2| &= 2 \\ |OB| &= ? \end{align}$$
OB uzunluğunun değeri nedir?

ABCD bir kare olduğuna göre soru işaretli açının değeri nedir?

$$ \begin{align} |DC| &= 2|EB| \\ |AB| &= |BD| \end{align}$$
Soru işaretli açının değeri nedir?

Bir tam daire içerisine iki yarım daire ile bir kare şekildeki gibi yerleştirilmiştir. Buna göre tam dairenin yarıçapı nedir?

ABCD karesinin alanı nedir?

ABCD bir kare olduğuna göre soru işaretli açının değeri nedir?

Soru işaretli açının değeri nedir?

AB uzunluğunun değeri nedir?

ABC dik üçgenini B köşesi etrafında 90o derece döndürerek
BB'A' dik üçgenini elde ediyoruz.
Buna göre, boyalı bölgenin alanının şeklin toplam alanına oranı nedir?

5 tane eş ikizkenar üçgen'den oluşan şekilde B1, A, C5 noktaları
doğrusaldır.
Buna göre, soru işaretli açının değeri kaçtır?

Maviye boyalı bölgenin alanı nedir?

Sarıya boyalı bölgenin alanı nedir?

ABC bir eşkenar üçgendir. Bu durumda |AD| uzunluğu nedir?


Ağırlık merkezi O noktası olan ABCD paralelkenarının D köşesini, Şekil I'de gösterildiği gibi AE doğrusu boyunca
kıvırıp Şekil II'yi elde ediyoruz.
$$ \begin{align} |OD'| &= 3 \\ |EC| &= 26 \end{align}$$
Buna göre |DE| uzunluğu nedir?
Alanı 24 olan ABCD paralelkenarında AE açıortayın uzunluğu nedir?

OBCD bir köşesi orjinde olan bir dikdörtgendir. Dikdörtgenin C köşesi EB boyunca kıvrıldığında
C' noktasına taşınmaktadır.
Dikdörtgenin C köşesinin koordinatları ile DE uzunluğu bilinmektedir.
Buna göre C' noktasından geçen d doğrusunun denklemi nedir?

𝑥 açısının değeri nedir?

|KL| uzunluğunun değeri nedir?

Çeyrek dairenin yarıçapı kaçtır?

Boyalı bölgenin alanı nedir?

Soru işaretli açının değeri nedir?

Boyalı bölgenin alanı nedir?

ABCD bir kare olduğuna göre soru işaretli açının değeri nedir?

Bir yarım daire içerisine şekilde görüldüğü gibi ikizkenar üçgenler çiziyoruz. Mavi açının değeri nedir?


ABCD bir karedir ve DC kenarı eşit parçalara bölünmüştür.
$$ \begin{align} |Dx_1| = |x_1x_2| = ... = |x_nC| &= |AP| \end{align}$$
$$ \begin{align} \sum_{k = 1}^{n + 1} \alpha_k &= ? \end{align}$$
𝑥 değişkeninin değeri nedir?

𝑥 açısının değeri nedir?

Soru işaretli açının değeri nedir?

|BC| uzunluğunun değeri nedir?

Maviye boyalı karenin alanı nedir?

Sarı, mavi ve yeşil üçgenlerin alanları soruda verilmiştir. Bu durumda pembe renge boyanmış üçgenin alanı nedir?

Bir eşkenar üçgenin köşeleri eş merkezli 3 çemberin her köşe bir çember üzerinde olacak şekilde yerleştirilmiştir. Eşkenar üçgenin bir kenar uzunluğunun parametrik gösterimi nedir?

$$ \begin{align} |AB| &= f(a,b,c) = ? \end{align}$$
Bu şekil kaç farklı şekilde çizilebilir?

Benzerlerinden biraz daha farklı bir soru!

Bu ispatı sadece geometri kullanarak yapacağız!

Bazen sondan başa ilerlemek sonuca gitmeyi kolaylaştırır!

Yukarıdaki sorunun düzeltmesi!

Çözüm için küçük bir numara gerekiyor!

Çemberin yarıçapı nedir?

Bir kare içerisinden rastgele seçilen bir P noktasını A ve B noktaları ile birleştiriyoruz. APB açısının 90 dereceden
büyük olma olasılığı nedir?

Çeyrek dairenin yarıçapı nedir?

Çevrel çemberin yarıçapı nedir?
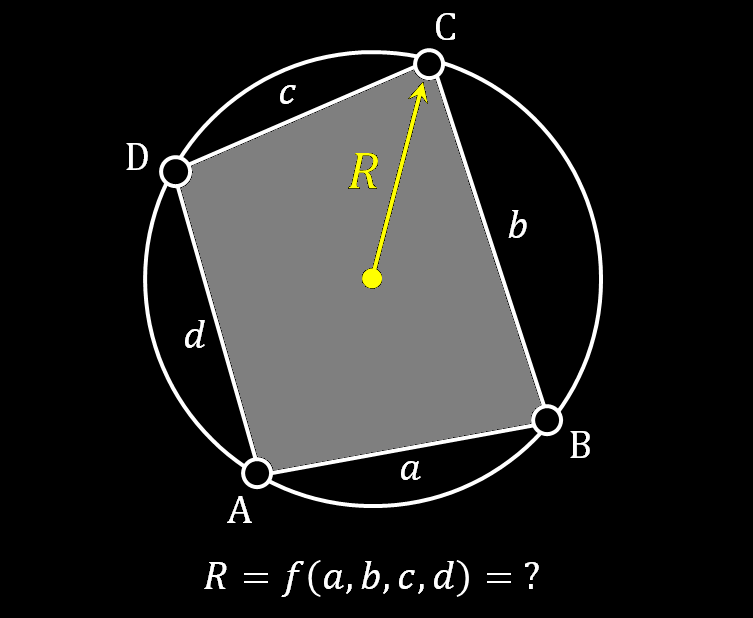
Trigonometri hayat kurtarır!
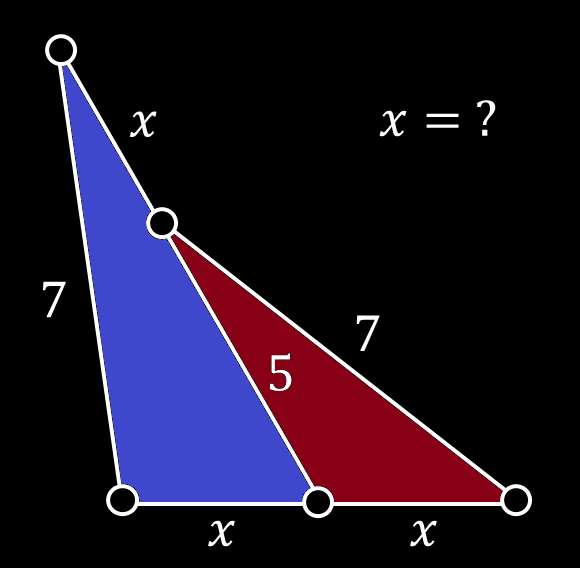
Daha pratik bir geometrik çözüm!

$$ \begin{align} x + \frac{1}{x} &= -1 \\ x^{2020} + \frac{1}{x^{2020}} &= ? \end{align}$$
$$ \begin{align} a + b + c &= 2022 \\ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} &= \frac{1}{2022} \end{align}$$
$$ \begin{align} \frac{1}{a^{2023}} + \frac{1}{b^{2023}} + \frac{1}{c^{2023}} &= ? \end{align}$$
$$ \begin{align} a,b \in \mathbb{Z}^{+} \end{align}$$
$$ \begin{align} a + b &= 20 \\ \text{max}\left\{ a^2 b \right\} &= ? \end{align}$$
$$ \begin{align} T &= 75 \times 30^2 \end{align}$$
İki basamaklı ardışık dört tek sayının rakamları çarpımı T sayısına eşittir. Bu durumda iki basamaklı sayılardan en küçüğü kaçtır?
Bir koninin yanal yüzeyi üzerindeki bir A noktasından başlayarak önce C noktasına kadar tırmanış, akabinde C noktasından B noktasına kadar bir iniş hareketi yapılıyor. Bu durumda |BC| uzunluğu nedir?

$$ \begin{align} f \: &: \: \mathbb{R} \rightarrow \mathbb{R} \\ f(x) f(y) &= f(x + y) + xy \\ f(x) &= ? \end{align}$$
$$ \begin{align} 34! = &295.232.799.\color{crimson}cd\color{black}9.604.140.847. \\ &618.609.643.5\color{crimson}ab\color{black}.000.000 \end{align}$$
Bu eşitliği sağlayan a,b,c,d rakamları nelerdir?
$$ \begin{align} \frac{2.244.851.485.148.514.627}{8.118.811.881.188.118.000} &= ? \end{align}$$
Bu işlemin sonucu kaçtır?
$$ \begin{align} \Bigl(3 + \text{cos}(x)\Bigr)^2 &= 4 - 2 \text{sin}^{8}(x) \end{align}$$
$$ \begin{align} 1 \cdot 2 \cdot 3 + 2 \cdot 3 \cdot 4 + ... + 97 \cdot 98 \cdot 99 &= ? \end{align}$$
$$ \begin{align} p,q \rightarrow \text{asal(prime)} \end{align}$$
$$ \begin{align} p^3 + q^3 + 1 &= p^2 q^2 \\ p,q &= ? \end{align}$$
$$ \begin{align} a,b \in \mathbb{N} \end{align}$$
$$ \begin{align} 2^a - 2^b &= 2016 \\ a,b &= ? \end{align}$$
$$ \begin{align} n,k \in \mathbb{Z} \end{align}$$
$$ \begin{align} (n + 1)^k - 1 &= n! \\ n,k &= ? \end{align}$$
$$ \begin{align} a,b \in \mathbb{N} \end{align}$$
$$ \begin{align} \sqrt{a} + \sqrt{b} &= \sqrt{2009} \\ a,b &= ? \end{align}$$
$$ \begin{align} a,b,c \in \mathbb{N} \end{align}$$
$$ \begin{align} \left(1 + \frac{1}{a}\right)\left(1 + \frac{1}{b}\right)\left(1 + \frac{1}{c}\right) &= 2 \\ a,b,c &= ? \end{align}$$
$$ \begin{align} \frac{p}{q} &= 1 - \frac12 + \frac13 - \frac14 + ... + \frac{1}{1319} \end{align}$$
p sayısının 1979 tarafından kalansız bölündüğünü ispatlayın.
$$ \begin{align} f \: : \: \mathbb{R} \rightarrow &\mathbb{R} \\ x,y,z \in &\mathbb{R} \end{align}$$
$$ \begin{align} f \Bigl(x^2 + y f(z)\Bigr) &= x f(x) + z f(y) \end{align}$$
Yukarıdaki bağıntıyı sağlayan tüm fonksiyonları bulabilir misiniz?
$$ \begin{align} x,y,z &\in \mathbb{N} \end{align}$$
$$ \begin{align} \frac{1}{x} + \frac{2}{y} - \frac{3}{z} &= 1 \\ x,y,z &= ? \end{align}$$
$$ \begin{align} f \: : \: \mathbb{R} &\rightarrow \mathbb{R} \end{align}$$
$$ \begin{align} g \Bigl(f(x + y)\Bigr) &= f(x) + (2x + y) g(y) \end{align}$$
Yukarıdaki bağıntıyı sağlayan tüm fonksiyonları bulabilir misiniz?
$$ \begin{align} f \: : \: \mathbb{Z}^{+} &\rightarrow \mathbb{Z}^{+} \end{align}$$
$$ \begin{align} f \Bigl(f(x)\Bigr) &= x + 1987 \end{align}$$
Yukarıdaki bağıntıyı sağlayan bir fonksiyonun olamayacağını ispatlayabilir misiniz?
$$ \begin{align} a,b,c &\in \mathbb{Z}^{+} \end{align}$$
$$ \begin{align} a! b! &= a! + b! + c! \\ a,b,c &= ? \end{align}$$
$$ \begin{align} \pi < \frac{22}{7} \end{align}$$
Yukarıdaki eşitsizliği ispatlayabilir misiniz?
$$ \begin{align} \frac{a - b}{c - d} &= 2 \\ \frac{a - c}{b - d} &= 3 \\ \frac{a - d}{b - c} &= ? \end{align}$$
$$ \begin{align} x,y &\in \mathbb{Z} \\ p &\in \mathbb{P} \: \text{(asal)} \end{align}$$
$$ \begin{align} x^2 - 3xy + p^2y^2 &= 12p \\ x,y,p &= ? \end{align}$$
$$ \begin{align} n,m &\in \mathbb{N} \end{align}$$
$$ \begin{align} 2^n + 3^n &= m^3 \end{align}$$
Yukarıdaki eşitliğin mümkün olamayacağını ispatlayabilir misiniz?
$$ \begin{align} n &\in \mathbb{N} \\ p &\in \mathbb{P} \end{align}$$
$$ \begin{align} 8^n + 47 &= p \end{align}$$
Yukarıdaki eşitliğin mümkün olamayacağını ispatlayabilir misiniz?
$$ \begin{align} n,m &\in \mathbb{Z} \end{align}$$
$$ \begin{align} \frac{8n - 25}{n + 5} &= m^3 \end{align}$$
Yukarıdaki eşitlik hangi şartlarda sağlanır?
$$ \begin{align} a,b,c,d &\in \mathbb{Z}^{+} \end{align}$$
$$ \begin{align} 4^a + 5^b + 6^c &= 7^d \\ a,b,c,d &= ? \end{align}$$
$$ \begin{align} a,b,c &\in \mathbb{Z}^{+} \end{align}$$
$$ \begin{align} a^3 + b^3 + c^3 &= (abc)^3 \\ a,b,c &= ? \end{align}$$
$$ \begin{align} a^2 + a &= b^3 + b \end{align}$$
a ve b aralarında asal iki sayıdır. Yukarıdaki eşitliği sağlayan sayılar hangileridir?
$$ \begin{align} m,n &\in \mathbb{N} \\ p &\in \mathbb{P} \: \text{(asal)} \end{align}$$
$$ \begin{align} m \Bigl( 4m^2 + m + 12 \Bigr) &= 3 \Bigl( p^n - 1 \Bigr) \\ m,n,p &= ? \end{align}$$

𝑥 uzunluğunun değeri nedir?

𝑥 uzunluğunun değeri nedir? (Alternatif çözüm)
$$ \begin{align} \frac{x}{21} &+ \frac{x}{77} + \frac{x}{165} + \frac{x}{285} \\ &+ \frac{x}{437} + \frac{x}{621} = 100 \end{align}$$
$$ \begin{align} x &= ? \end{align}$$
$$ \begin{align} a,b,c \in \mathbb{Z} \end{align}$$
$$ \begin{align} ab + c &= 2020 \\ a + bc &= 2021 \\ a,b,c &= ? \end{align}$$
$$ \begin{align} f(x) &= \text{sin}(2x)\text{sin}(3x)\text{sin}(5x)\text{sin}(30x) \\ g(x) &= \text{sin}(x)\text{sin}(6x)\text{sin}(10x)\text{sin}(15x) \end{align}$$
$$ \begin{align} \int_{0}^{\pi} \left(\frac{f(x)}{g(x)}\right) dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\frac{\pi}{2}} \left(\frac{\sqrt[3]{\text{tan}(x)}}{\Bigl(\text{sin}(x) + \text{cos}(x)\Bigr)^2}\right) dx &= ? \end{align}$$
$$ \begin{align} f(x) &= x^2 + 1 \\ g(x) &= x^4 + x^2 + 1 \end{align}$$
$$ \begin{align} \int_{-\frac12}^{+\frac12} \left(\sqrt{f(x) + \sqrt{g(x)}}\right) dx &= ? \end{align}$$
$$ \begin{align} 10^{20}\int_{2}^{\infty} \left(\frac{x^9}{x^{20} - 48x^{10} + 575}\right) dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} \left(\sum_{n = 1}^{\infty} \frac{\left \lfloor 2^n x \right \rfloor}{3^{n}} \right)^2 dx &= ? \end{align}$$
$$ \begin{align} m \in \mathbb{Z} \end{align}$$
$$ \begin{align} 3^m - 2^m &= 65 \\ m &= ? \end{align}$$
Hangisi büyüktür?
$$ 50^{50} \: \unicode{x2753} \: 49^{51}$$
$$ \begin{align} p,q,r &\in \mathbb{P} \: \text{(asal)} \\ m &\in \mathbb{N} \end{align}$$
$$ \begin{align} \frac{1}{p} + \frac{1}{q} + \frac{1}{r} &= \frac{1}{m} \\ p,q,r,m &= ? \end{align}$$
İki arkadaş Kızıl Meydan'da buluşmaya karar verirler. Her ikisi de 12:00 ile 13:00 arasında herhangi bir anda
bu meydana gelecekler, 15 dakika bekleyip gideceklerdir.
Bu 15 dakikalık süre zarfında birbirlerine rastlarlarsa buluşmuş olacaklar. Bu durumda bu iki arkadaşın buluşma olasılığı nedir?
$$ \begin{align} 8^x + 2^x &= 130 \\ x &= ? \end{align}$$
$$ \begin{align} 3^x + x &= 30 \\ x &= ? \end{align}$$
$$ \begin{align} x,y &\in \mathbb{R} \end{align}$$
$$ \begin{align} x^y &= y^x \\ x,y &= ? \end{align}$$
$$ \begin{align} \left( \frac{4x}{3x + 1} \right)^3 - \left( \frac{x - 1}{3x + 1} \right)^3 &= 1 \end{align}$$
$$ \begin{align} x &= ? \end{align}$$
$$ \begin{align} x^2 - x^3 &= 12 \end{align}$$
$$ \begin{align} x &= ? \end{align}$$
$$ \begin{align} a > b \: &\wedge \: a,b \in \mathbb{R} \end{align}$$
$$ \begin{align} 2^a + 2^b &= 75 \\ 2^{-a} + 2^{-b} &= 12^{-1} \end{align}$$
$$ \begin{align} a,b &= ? \end{align}$$
$$ \begin{align} x,y \in \mathbb{R} \end{align}$$
$$ \begin{align} x + y &= 4 \\ x^5 + y^5 &= 464 \end{align}$$
$$ \begin{align} x,y &= ? \end{align}$$
$$ \begin{align} \frac{73^3 + 34^3}{73^3 + 39^3} &= ? \end{align}$$
$$ \begin{align}
xy + z &= 40 \\
xz + y &= 51 \\
x + y + z &= 19
\end{align}$$
$$ \begin{align} \int \frac{e^{x/2} \text{cos}(x)}{\sqrt[3]{3 \text{cos}(x) + 4 \text{sin}(x)}} dx &= ? \end{align}$$
$$ \begin{align} n \geq 0 \end{align}$$
$$ \begin{align} u(x) &= \bigl \lfloor 2^n x \bigr \rfloor \\ v(x) &= \bigl \lfloor 2^n x -\frac14 \bigr \rfloor \end{align}$$
$$ \begin{align} \int_{0}^{1} \text{max} \Bigl[ \frac{1}{2^n} \Bigl( u(x) - v(x) \Bigr) \Bigr] dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \frac{\ln\left(2e^x - 1 \right)}{e^x - 1} dx &= ? \end{align}$$
$$ \begin{align} u(x) &= \sqrt[3]{1 + \sqrt{1 - x^3}} \\ v(x) &= \sqrt[3]{1 - \sqrt{1 - x^3}} \end{align}$$
$$ \begin{align} \int_{-1/3}^{1} \bigl( u(x) + v(x) \bigr) dx &= ? \end{align}$$
$$ \begin{align} \int_{-\infty}^{\infty} \frac{1}{x^4 + x^3 + x^2 + x + 1} dx &= ? \end{align}$$
$$ \begin{align} \sum_{n=1}^{90} \frac{(2n) \text{sin}(2n^{\circ})}{90} &=? \end{align}$$
$$ \begin{align} \frac{x^2 y + x y^2}{x^2 + y^2 + 1} &= 1 \end{align}$$
$$ \begin{align} x,y &\in \mathbb{Z} \end{align}$$
$$ \begin{align} \frac{1}{x} &= \frac{7 + \sqrt{91} + 7\sqrt{7} + 7\sqrt{13}}{14 + \sqrt{91} + \sqrt{7}} \end{align}$$
$$ \begin{align} x^6 &= ? \end{align}$$
$$ \begin{align} n 2^n + 1 &= \text{Perfect Square} \end{align}$$
$$ \begin{align} a * b &= ab + a + b \end{align}$$
$$ \begin{align} 1 * (2 * (3 * (4 \; * \; ... * \; (99 * 100)))) &= ? \end{align}$$
$$ \begin{align} (n - 1)! + 1 &= n^2 \end{align}$$
$$ \begin{align} pqr &= 59(p + q + r) \end{align}$$
$$ \begin{align} p,q,r &\in \mathbb{P} \end{align}$$
$$ \begin{align} (\sqrt{2} - 1)^{12} &= ? \end{align}$$
$$ \begin{align} n! + 8 &= 2^k \end{align}$$
$$ \begin{align} n,k \in \mathbb{Z} \end{align}$$
$$ \begin{align} \left(x^2 - y^2\right)^2 &= 1 + 16y \end{align}$$
$$ \begin{align} x,y \in \mathbb{Z} \end{align}$$
$$ \begin{align} n \: \text{&} \: \sqrt{n^2 + 204n} \in \mathbb{Z}^{+} \end{align}$$
$$ \begin{align} \text{max}(n) &= ? \end{align}$$
$$ \begin{align} 8^x &= 6x \end{align}$$
$$ \begin{align} 5^k &= k^{625} \end{align}$$
$$ \begin{align} 4^{8} - 1 \:\:\: &\text{&} \:\:\: 8^{12} - 1 \end{align}$$
$$ \begin{align} \text{GCF} = \text{EBOB} &= ? \end{align}$$
$$ \begin{align}
f(x) &= \text{sin}(20x) + 3 \text{sin}(21x) + \text{sin}(22x) \\
g(x) &= \text{cos}(20x) + 3 \text{cos}(21x) + \text{cos}(22x)
\end{align}$$
$$ \begin{align} \int \sqrt{f^2(x) + g^2(x)} dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{\infty} \frac{e^{-2x} \text{sin}(3x)}{x} dx &= ? \end{align}$$
$$ \begin{align} \int_{0}^{1} x^{1/3} (1 - x)^{2/3} dx &= ? \end{align}$$
$$ \begin{align} f(x) &= \text{cos}(2022 x) \\ g(x) &= \frac{\text{sin}(10050 x)}{\text{sin}(50 x)} \\ h(x) &= \frac{\text{sin}(10251 x)}{\text{sin}(51 x)} \end{align}$$
$$ \begin{align} \int_{0}^{2 \pi} f(x) g(x) h(x) dx &= ? \end{align}$$
$$ \begin{align} \left \lfloor \log_{10} \left( \int_{2022}^{\infty} e^{-x^3} dx \right) \right \rfloor &= ? \end{align}$$
Tamkare farkı ile pratik ama eksik çözüm!
$$ \begin{align} a^b - b^a &= 17 \end{align}$$
$$ \begin{align} a,b &\in \mathbb{Z}^{+} \end{align}$$
Olası durumlar analizi ve genel çözüm!
$$ \begin{align} a^b - b^a &= 17 \end{align}$$
$$ \begin{align} a,b &\in \mathbb{Z}^{+} \end{align}$$
$$ \begin{align}
\int e^{\text{cos}(x)} \text{cos}\Bigl( 2x + \text{sin}(x) \Bigr) dx &= ?
\end{align}$$
$$ \begin{align}
\int \text{tan}(x) \sqrt{2 + \sqrt{4 + \text{cos}(x)}} dx &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{\infty} \frac{dx}{\left( x + 1 + \lfloor 2 \sqrt{x} \rfloor \right)^2} &= ?
\end{align}$$
$$ \begin{align}
\int_{0}^{10} \left \lfloor \left(\frac{1 + \sqrt{5}}{2} \right)^{\lfloor x \rfloor} \right \rfloor dx &= ?
\end{align}$$
$$ \begin{align}
f(x) &= \max(|2\text{sin}(x)|, |2\text{cos}(2x) - 1|) \\
g(x) &= \min(|\text{sin}(2x)|, |\text{cos}(3x)|)
\end{align}$$
$$ \begin{align}
\int_{0}^{\pi} f^2(x) g^2(x) dx &= ?
\end{align}$$
$$ \begin{align}
f(x) &= \sqrt{\frac{1}{4x^2} + \frac{1}{x} - x} \\
g(x) &= \sqrt{\frac{x^4}{4} - x + 1} + \frac{1}{2x}
\end{align}$$
$$ \begin{align}
\int_{0}^{1} \Bigl( f(x) - g(x) \Bigr) dx &= ?
\end{align}$$
$$ \begin{align}
\sqrt{5} + \sqrt{6} + \sqrt{7} + ... + \sqrt{13}
\end{align}$$
Yukarıdaki işlemin sonucunun tamsayı kısmı kaçtır?
Bu soruda tahmin yapmak yok!
$$ \begin{align}
\sqrt{4.444.222.225}
\end{align}$$
Hesap makinası kullanmak yasak!
$$ \begin{align}
x + \frac{3x - y}{x^2 + y^2} &= 3 \\
y - \frac{x + 3y}{x^2 + y^2} &= 0
\end{align}$$
Tüm (x, y) çiftlerini arıyoruz.
$$ \begin{align}
n_1 + n_2 + n_3 \; + \; ... \; &= 1976
\end{align}$$
$$ \begin{align}
n &= n_1 \times n_2 \times n_3 \; \times \; ...
\end{align}$$
$$ \begin{align}
n_i \in \mathbb{Z}^{+} \Rightarrow max(n) &= ?
\end{align}$$